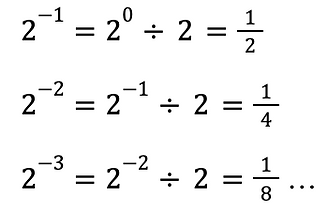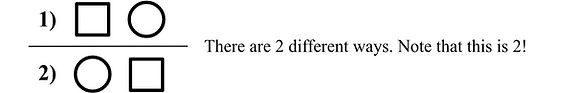First of all, let’s define factorial. Factorial is a function of any natural number that multiplies all the counting numbers less than or equal to itself. The factorial of the number “n” is represented as n! and it is equal to the following expression:

​

​

​

In maths, we sometimes encounter situations that seem illogical and odd. We often get confused, wonder why is that the case, or argue the accuracy of the mathematical model in question. In such cases, we should consider that there exists a rule which results in the given model, and the rule has no reason to be disobeyed. What do I mean by that? Let’s discuss an example before diving into the actual question. 

 

We learned in middle school that           . Let’s be honest, we all found this ridiculous at first. Maybe we still do. But there is a pattern that gives us this equation, and that pattern is not broken in any case. Choose a number, be lazy and choose 2.

​

​

​

​

​

​

 

By increasing the power by 1, we multiply the previous number by 2. For example,                           and                            . If we go backward, by decreasing the power by 1, we divide the previous number by 2. For example,                         and                       . The same rule applies to       .

 

 

 

 

 

​

​

 

You see. When we apply the pattern of dividing the exponential number by the base by decreasing the power by 1, we obtain                                      . Although it seems weird at first glance, following the pattern results in the notion that any number to the power of 0 equals 1. If we continue with the negative powers, the pattern gives us something really familiar.

​

​

​

​

​

​

​

​

​

​

​

Similarly, we will approach 0! by following the pattern mathematicians created, and we will also see that this applies to the real world, though a little philosophically. We are now in the field of permutations. Permutations refer to in how many different ways can a given set be ordered. Guess what? We use factorial to find the number of different arrangements. Let's visualize…

 

Given a circle and square, how many arrangements are there?

 

Now, we have 3 shapes: a circle, a square, and a triangle. How many different orders are there?

 

We will come back to this example later. Now, we will apply the patterns we will discover to prove that 0!=1. 

​

​

​

​

​

​

​

​

​

​

​

 

By decreasing the number one by one, what we are actually doing is dividing the previous factorial by its coefficient. For example,                                                 . One more,                                                   . Why wouldn’t the rule apply to zero factorial? There is just no reason for it to break down. This gives us…

​

​

​

Another pattern we might notice is n! = n(n-1)! Example: 5! = 5 x 4! = 5 x 24 = 120

If we apply the rule, we obtain again,

​

​

​

​

 

Let’s go back to the example with the shapes. We discussed that n! gives us the number of different arrangements of a set containing n elements. When there are 10 elements, we can order them in 10! different ways. I have a question: what would give us the number of arrangements of a set which contains no elements? Yes sir, it is 0! In other words, 0! gives us how many ways there are to order nothing. I said it is a little bit philosophical, but nobody would argue that there is only “one way” to arrange nothing, which is “not arranging” or doing nothing. 

 

As you can see, we proved a famous and commonly questioned notion, 0! = 1, by following the patterns of mathematics. We also saw that this notion makes sense in real life. 

​

​

References

Numberphile, director. Zero Factorial - Numberphile. YouTube, YouTube, 8 June 2013, https://www.youtube.com/watch?v=Mfk_L4Nx2ZI. Accessed 14 Jan. 2023. 

Misterwootube, director. Why Is 0! = 1? YouTube, YouTube, 30 Apr. 2014, https://www.youtube.com/watch?v=X32dce7_D48. Accessed 14 Jan. 2023.

Estela, Mike. “Zero Factorial.” ChiliMath, 30 May 2022, https://www.chilimath.com/lessons/intermediate-algebra/zero-factorial/.